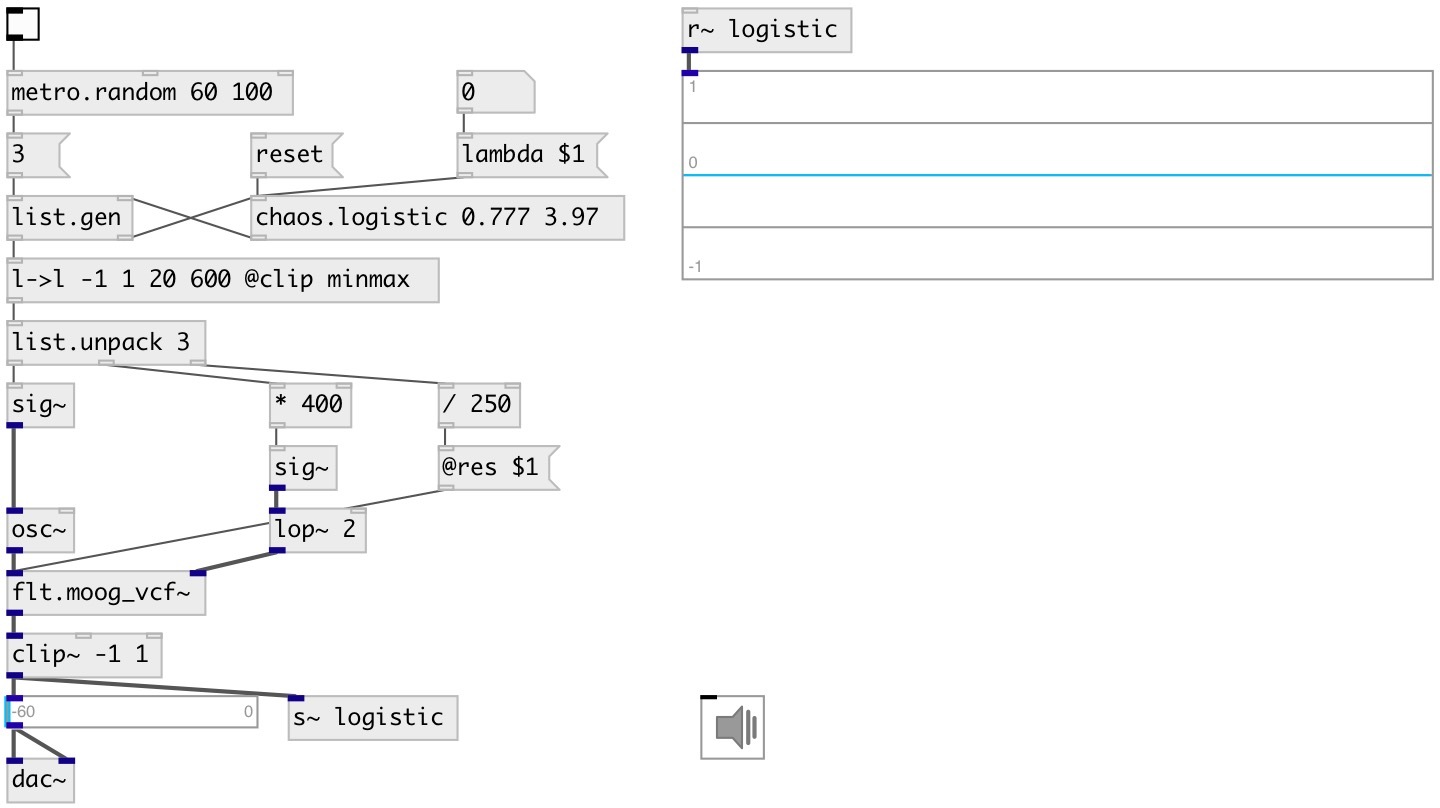
index :: chaos

chaos.logistic

Logistic map chaotic generator

доступно с версии: 0.9

---

информация

A non-interpolating generator based on the difference equations: x[n+1] = λ * x[n] * (1 - x[n]) By varying the parameter λ, the following behavior is observed: • With λ between 0 and 1, the population will eventually die, independent of the initial population • With λ between 1 and 2, the population will quickly approach the value λ − 1/λ, independent of the initial population • With λ between 2 and 3, the population will also eventually approach the same value λ − 1/λ, but first will fluctuate around that value for some time. • With λ between 3 and 1 + √6 ≈ 3.44949, from almost all initial conditions the population will approach permanent oscillations between two values. These two values are dependent on λ. • With λ between 3.44949 and 3.54409 (approximately), from almost all initial conditions the population will approach permanent oscillations among four values. • With λ increasing beyond 3.54409, from almost all initial conditions the population will approach oscillations among 8 values, then 16, 32, etc. • At λ ≈ 3.56995 is the onset of chaos, at the end of the period-doubling cascade. • Most values of r beyond 3.56995 exhibit chaotic behavior, but there are still certain isolated ranges of r that show non-chaotic behavior. Beyond λ = 4, almost all initial values eventually leave the interval [0,1] and diverge.

аргументы:

• INIT x init value (default 0.777)
  тип: float
  

• LAMBDA lambda value (default 3.9)
  тип: float
  

методы:

• lambda set lambda value
  

• om set output mode.
  параметры:
  • BOOL output mode. If 1: outputs new generated value after lambda or seed method call, if 0 - change values without output. Default is 0.
    тип: int
    обязательно: True
    

• reset set to initial state
  

• seed set init value, updates init value
  

• set set init value and lambda value and updates init value
  

входы:

• generate and output new value
  тип: control

выходы:

• new generated x-value
  тип: control

ключевые слова:

chaos logistic

Смотрите также: [chaos.std0]

Авторы: André Sier

Лицензия: GPL3 or later